שלום וברכה 👋
עשיתי בעבר מדריכים על חיזוי אוטומטי הפעם אני רוצה לדבר על נושא קרוב, אך לא אותו דבר, על רגרסיה ליניארית.

רגרסיה מתאימה כאשר יש לך נתונים שבהם אתה חושב שקיים קשר בין משתנים.
דוגמה פשוטה - מתי צריך רגרסיה היא זו:
אם יש לי דוכן גלידה 🍦, ואני משער שכמות הגלידה תלויה בטמפרטורה 🌡️. אז רגרסיה יכולה להוכיח שזה נכון, לאשש את ההשערה שלי, או לפסול אותה.
כלומר באמצעות רגרסיה אפשר למצוא קשר בין 2 משתנים (או יותר). להבין האם משהו אחד משפיע על משהו אחר, ובאיזו עוצמה הוא משפיע.

דוגמה אמיתית נוספת שנתקלתי בה וממחישה את הצורך ברגרסיה היא זו: מור, היא בעלת חנות אונליין קטנה 🛒, עם תקציב פרסום מוגבל. למור היה נוהל, שפעם בחודש היא שלחה ללקוחות היקרות שלה ברשימת התפוצה קופונים להנחות, אבל זה לא תמיד עבד. כמובן, היו לקוחות שהתלהבו וקנו, והיו כאלה שהתעלמו.

מור החליטה לבדוק את זה בצורה מבוססת נתונים 📊.

מור הצליחה ללקט מ- Google Analytics את הנתונים הבאים:

• תדירות ביקורים באתר
• הוצאה ממוצעת של כל לקוחה
• האם הלקוחה הגיבה לקופונים בעבר (זה נתון שהצריך קצת עבודת הכנה באקסל, אבל היא הצליחה).

יחד עם הנתונים שהיו לה, מור ביצעה ניתוח רגרסיה ליניארית פשוטה.
המטרה הייתה להשתמש ברגרסיה כדי לבדוק האם “תדירות ביקורים” משפיעה על “שימוש בקופונים”.

ניתוח רגרסיה ליניארית פשוט גילה למור משהו מאוד מעניין:
ישנן לקוחות שההנחה מזיזה להם הכול – תן להן 10% הנחה והן מייד קונות. אבל ישנן לקוחות מסוג אחר, שהקופון פשוט לא משפיע עליהן. אפשר לומר, שהלקוחות מהסוג השני כבר נאמנות למותג – הן לא צריכות מבצע בשביל להזמין שוב.

המסקנה הזו ששינתה את צורת העבודה של מור: במקום לשלוח לכולם את אותו הדוא"ל עם הקופון, מור ביצעה חלוקה של הלקוחות ל-2 קבוצות:

לקוחות רגישות למחיר (כאלו שהגיבו בעבר לקופונים, אך לא ביקרו בתדירות גבוהה בלי הקופונים): הן קיבלו קופונים יותר שווים, כלומר הנחה אגרסיבית יותר.
לעומתן, לקוחות נאמנות: קיבלו קמפיינים רכים יותר – כמו הודעה על מוצרים חדשים או סיפורים מעניינים על התחום.

התוצאה הייתה מדהימה 🚀: שיעור ההמרה בקמפיינים קפץ משמעותית. כך, תקציב הפרסום הוקצה בצורה מדויקת – בלי לבזבז קופונים על מי שלא צריכה אותם.

והכי חשוב – נוצרו יחסים עמוקים יותר עם לקוחות נאמנים 🤝.

💡 המסקנה: רגרסיה ליניארית אולי נשמעת מסובכת, משהו שחייבים ללמוד בקורסי סטטיסטיקה ואחר כך שוכחים ממנו. אבל בפועל, יש לה כוח חזק מאוד, היא יכולה לעזור לעסק בכל גודל לקבל החלטות חכמות, להפסיק לנחש, ולהתחיל להבין מה באמת מניע את הלקוחות שלו, או בכלל תובנות אחרות על העסק.

בואו נלמד רגרסיה ליניארית ונגלה יחד איך זה יכול לעזור גם לך. לך תדע, אולי הרגרסיה הבאה שלך תביא אותך למסקנה, שתחסוך לך אלפי שקלים…💸

הערה חשובה מאוד: המטרה שלי כאן היא שכל אחד יוכל לדעת להשתמש ברגרסיה ליניארית ומתי אפשר לסמוך על הרגרסיה הליניארית שיצאה, ומתי לא. כשאני אומר כל אחד, אני מתכוון לכל אחד - בין אם הוא בעל עסק סטודנט קורא אקראי באתר תותח אקסל.

המטרה שלי היא לא ללמד סטטיטיקה, ולכן, אני בוחר במודע ניסוחים יותר פשוטים וברורים, אך לאו דווקא מדוייקים מבחינה אקדמית.
מהסיבה הזו בדיוק, אני גם אתן פה בהמשך המדריך “כללי אצבע” 📝, ואצמד אליהם.
ומהסיבה הזו, אני אתמקד במקרה הפשוט ביותר, שבו אנחנו משערים שיש דבר אחד שמשפיע על התחזית שלנו (ולא הרבה דברים).
המטרה היא שכל אחד מכם שמשקיע את הזמן היקר שלו בסרטון שלי. אז כאשר יגיע הרגע שבו קופץ לכם בראש רעיון, שמשהו מסויים משפיע על משהו אחר (בעסק או בכל תחום אחר), במקרה כזה, יהיה לכם את הידע לפתוח אקסל ולבדוק אם זה נכון או לא. ובצורה הזו - לבסס את ההחלטות שלכם, על נתונים, ולא על תחושות בטן.
וכל זאת, מבלי להבין לעומק את הסטטיסטיקה שמאחורי המודל.

מה זה רגרסיה ליניארית ? 🤔

רגרסיה ליניארית

• זו שיטה סטטיסטית 📈
• השיטה הזו מאפשרת לחזות ערך באמצעות משתנה.
• כלומר אנחנו אם אנחנו משערים שמשהו משפיע על תוצאה מסויימת, אז השיטה הזו תעזור לנו להעריך מה תהיה התוצאה אם נעשה יותר/פחות מהדבר הזה.

מה מקור השם “רגרסיה” ? 🧬

בן דוד של דארווין, פרנסיס גולטון ביצע מחקר ב 1885, וגילה תופעה מעניינת: בנים שנולדו להורים גבוהים, מושפעים מהגובה של הוריהם, כלומר הילדים של ההורים הגבוהים, באמת היו גבוהים יותר מהממוצע, אבל, לא גבוהים כמו הוריהם.
הוא נתן שם לתופעה “רגרסיה לממוצע”, כלומר, מגמה שקיימת של נסיגה, התכנסות אל הממוצע.

מה המשמעות של “ליניארית” בביטוי רגרסיה ליניארית? ➡️

• בשיטת רגרסיה לינארית, אנחנו מניחים שקיים קשר לינארי (ישר) בין משהו אחד למשהו אחר.
• קשר לינארי משמעותו: ככל שנעשה יותר ממשהו אחד, נקבל יותר ממשהו אחר.
  • וגם להפך כמובן, ככל שנעשה פחות ממשהו אחד, נקבל פחות מהדבר השני.
• למשל, הקשר במשפט הבא הוא קשר ליניארי:
  • ככל שנשים יותר סוכר בתה, כך התה יהיה מתוק יותר.
• צריך להדגיש שזוהי שיטה לתחזית.
  כלומר, עצם העובדה שנשתמש ברגרסיה ליניארית לא תגרום למציאות להסתדר באמת בקו ישר, ליניארי. אלא, שהכלי שנקרא רגרסיה ליניארית מסייע לנו להעריך, לחזות ערך שסביר שיקרה במציאות אם נשנה משהו מסויים.

דוגמאות רגרסיה להמחשה:

• ככל שהורה גבוה, אז הילד שיוולד לו גם יהיה גבוה במידה דומה.
• כל שקל שנשקיע יותר בפרסום דרך Google Ads, יתן לנו רווח נוסף של 1.5 ש"ח.
• כל 1 ש"ח שחברת Moko Pharm מפחיתה את מחיר החיתולים בחנות, גורם ללקוחות לקנות סל ממוצע גבוה יותר ב-2 ש"ח.

כלומר, יש לנו משתנה אחד שמאפשר לנו לחשב = לנבא = לחזות משתנה אחר.
מקובל לקרוא לצמד המשתנים האלו כך:

• משתנה מסביר - כי הוא מסביר את התוצאה.
• משתנה מוסבר - שאותו אנחנו מעוניינים לחזות.

כאן המקום לציין שיש כל מיני סוגים של ניתוחי רגרסיה. במדריך הזה, אני אתמקד ספציפית ברגרסיה לינארית במשתנה יחיד.
משתנה יחיד, הכוונה - שאנחנו בודקים השפעה של משתנה אחד בלבד. אך עלי לציין, שכדי לבדוק מספר משתנים, זה ממש קל באקסל, ברגע שמבינים איך משתנה אחד עובד.

דוגמה להמחשה של המושגים “משתנה מסביר” ו- “משתנה מוסבר”

מור היקרה שלנו, קנתה זיכיון ופתחה גלידריה 🍨. היא הבינה עם הזמן שככל שהטמפרטורה עולה - היא מוכרת יותר גלידות - זו רגרסיה במשתנה יחיד. המשתנה המסביר, הוא טמפרטורה, והמשתנה המוסבר הוא כמות גלידות.

דוגמה להמחשת רגרסיה עם יותר ממשתנה אחד

אבל…. לצורך הדוגמה, נניח שמור מגלה לתדהמתה שגם גיל המוכרנים משפיע על המכירות (מוכרים/ות צעירים יותר, מצליחים למכור יותר כדורי גלידה). במקרה זה יש לנו 2 משתנים מסבירים: טמפרטורה+גיל המוכרים. זוהי רגרסיה במספר משתנים.

מה התוצאה של רגרסיה ליניארית? מה התוצר הסופי של רגרסיה ליניארית? 🎯

כשאנחנו אומרים שרגרסיה זו שיטה סטטיסטית, שעוזרת לנו לחזות משהו. אז מה בעצם התוצר שלה?
התוצר של רגרסיה הוא נוסחת חיזוי.
הנוסחה נראית כך:

Y = b + aX  

המשתנה y הוא התחזית, כלומר כמה אנחנו משערים שתהיה התוצאה אם יהיה x במציאות.

למשל-
אם נשקיע 1000 ש"ח (זה ה x, כלומר המשתנה המסביר) בפרסום אז הרווחים שלנו יהיו 2000 ש"ח (זה ה y - המשתנה המוסבר, המשתנה הלא ידוע, שאותו אנחנו נרצה לחזות באמצעות הנוסחה).

נסביר גם את b ואת a.

אנחנו מנסים באמצעות רגרסיה, לחזות ערכים מסויימים במציאות.
אז כאשר מציירים את קו הרגרסיה, לקו יש שיפוע מסויים - זהו ה x .
ואותו קו, מתחיל מנקודה מסויימת במרחב - זהו b.

לפעמים, יש גם הסבר ברור במציאות למשתנים האלו, ולפעמים לא.
בסופו של דבר, קו=נוסחת הרגרסיה הוא מודל שעוזר לנו לחזות ערכים בהינתן x מסויים.
הוא לא מבטיח שהערכים יהיו כמצופה, אלא שאם אנחנו משערים שיש במציאות תבנית מסויימת, אז הוא מסייע לנו לנסח את התבנית באמצעות נוסחה - והנוסחה הזו, היא התוצר הסופי שלנו , היא מה שאנחנו מחפשים.

איך מחשבים רגרסיה ליניארית באקסל ? 🧮

אני אציג כאן 4 שיטות לחישוב רגרסיה ליניארית ב- Excel.

• שיטה אחת באמצעות הוספת קו מגמה לגרף
• שיטה שניה - באמצעות 2 נוסחאות, שמחשבות עבורנו את השיפוע והחותך, ואז נבנה את נוסחה הרגרסיה בעצמנו.
• שיטה שלישית - באמצעות נוסחה בודדת שמחשבת פשוט את התחזית לנקודה ספציפית.
• שיטה רביעית - באמצעות התוסף Analysis Toolpack.

אציין מראש, שעדיף להשתמש בשיטה השלישית, כלומר עם התוסף Analysis Toolpack. מכיוון שהתוסף מייצר גם עוד כמה מדדים, שמסייעים לנו להעריך עד כמה נוסחת הרגרסיה שלנו אמינה.

איך להוסיף קו מגמה לגרף אקסל? 📊

השיטה הראשונה, ממש פשוטה.

• מסמנים את הנתונים של המשתנה המוסבר והמשתנה המסביר (2 עמודות אקסל באותו אורך)
• הוספה > גרפים מומלצים > בוחרים בגרף נקודות (הראשון שמופיע).
• בגרף לוחצים מקש ימני על הנקודות > הוספת קו מגמה
• בתפריט הצדדי שנפתח, נבחר באפשרות “ליניארית”, ונסמך ב-V את האפשרות הצג נוסחה.

איך לחשב רגרסיה ליניארית ב Excel באמצעות נוסחאות ? 📝

לצורך הנוסחאות, צריך לדעת להבדיל בין משתנה מוסבר למשתנה מסביר כמו שכתבתי למעלה.

כיוון שנוסחת הרגרסיה שלנו היא בעצם במבנה קבוע, שתמיד תכיל שיפוע+חותך. אז:

• כדי לחשב את השיפוע - נשתמש בנוסחת אקסל SLOPE.
• כדי לחשב את החותך - נשתמש בנוסחת אקסל INTERCEPT.

2 פונקציות אקסל אלו, עובדות באותה צורה:

• הפרמטר הראשון - כל סדרת הנתונים של המשתנה המוסבר שכבר ידועים לנו.
• הפרמטר השני - כל ערכי המשתנה המסביר.

ואז נשתמש בנוסחת slope. ובנוסחת intercept

נוסחת SLOPE

=SLOPE(a-כל_סדרת_הנתונים_של_המשתנה_המסביר , b-כל_סדרת_הנתונים_של_המשתנה_המוסבר)

נוסחת INTERCEPT

=INTERCEPT(a-כל_סדרת_הנתונים_של_המשתנה_המסביר , b-כל_סדרת_הנתונים_של_המשתנה_המוסבר)  

כתיבת נוסחת הרגרסיה

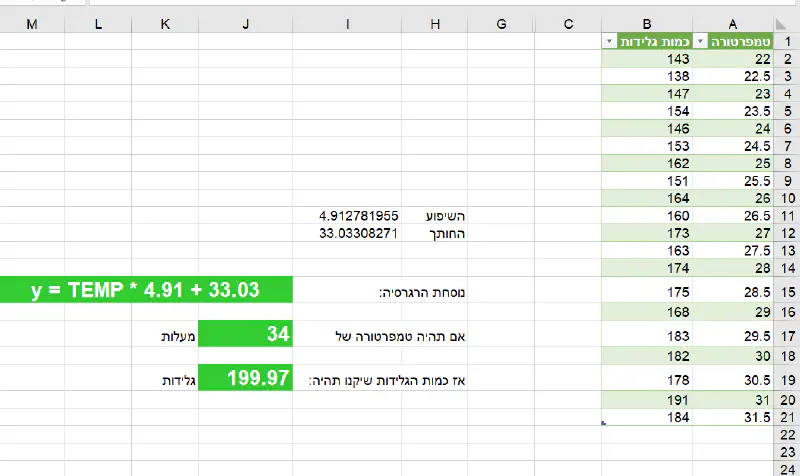
כעת, אחרי שחישבנו את השיפוע והחותך, פשוט נרשום את הנוסחה:

תחזית = שיפוע * משתנה מסביר + חותך

Y= a*x + b

זוהי נוסחת הרגרסיה שלנו.

שימוש בנוסחת הרגרסיה שיצרנו

כעת, ניקח לדוגמא מצב שבו הקיץ הישראלי הגיע, והטמפרטורה, כלומר x , המשתנה המסביר היא 34 מעלות.
ופשוט נציב את x בנוסחה שיצרנו, על מנת לקבל תחזית ל y מתאים.

y = 34* 4.91 + 33.03  

כמות הגלידות שיקנו באותו יום, תהיה כ-200 גלידות (199.97).
כעת מור, בעלת חנות הגלידות, יודעת על בסיס נתונים, כיצד להיערך נכון.

שילוב הנוסחאות האלו, נותן לנו רגרסיה ליניארית בצורה של החישובים הבסיסיים. אנחנו מחשבים “בעצמנו” כל מרכיב בנוסחה.
יש בזה חיסרון - זה הרבה עבודה. ויותר חשוב, אין לנו פה את המדדים שעוזרים להבין האם הרגרסיה הליניארית שחישבנו אמינה מספיק במקרה זה. לכן עדיף להשתמש בשיטה השלישית שאציג שעובדת באמצעות התוסף Analysis Toolpack.

שיטה 2 - נוסחת אקסל לחישוב רגרסיה ליניארית

השיטה הזו ממש פשוטה, באמצעות נוסחת FORECAST.LINEAR. נוסחה זו מחשבת לבד את ה y הרצוי, אך, לא מציגה את נוסחת הרגרסיה.

הערה: בגירסאות אקסל קודמות, נוסחה זו נקראה FORECAST וכעת שם הנוסחה הוחלף ל- FORECAST.LINEAR.

נדגים עם אותם נתונים בדיוק, כיצד לחזות ערך y כלשהוא:

קיבלנו תוצאה דומה מאוד (שונה מעט בגלל ענייני עיגול).

=FORECAST.LINEAR(34,glass[כמות גלידות],glass[טמפרטורה])  

גם כאן, יש חסרונות בשימוש בנוסחת FORECAST.LINEAR של Excel:

• כיוון שאנחנו עוסקים בנוסחת חיזוי, אז יש חשיבות גם למדדים שמודדים את עוצמת הקשר בין המשתנים.
• ולכן, שימוש ישירות בנוסחת רגרסיה ליניארית FORECAST.LINEAR בלי לחשב גם את המשתנים שמצביעים על עוצמת הקשר - עשוי לגרום לנו לטעות בגדול, ולחזות ערכים שלא קשורים אחד לשני בצורה מספיק חזקה שמאפשרת תחזית הגיונית מבחינה מקצועית (סטטיסטית).

לכן - עדיף להשתמש בשיטה הבאה, באמצעות התוסף Analysis Toolpack.

חישוב רגרסיה ליניארית באקסל עם Analysis Toolpack 🧰

איך מתקינים על אקסל את התוסף Analysis Toolpack? ⚙️

ראשית נתקין את תוסף Analysis Toolpack על אקסל.

• נלחץ על תפריט קובץ File
• נבחר ב- אפשרויות Options
• נבחר ב- תוכניות עזר Excel Add-ins
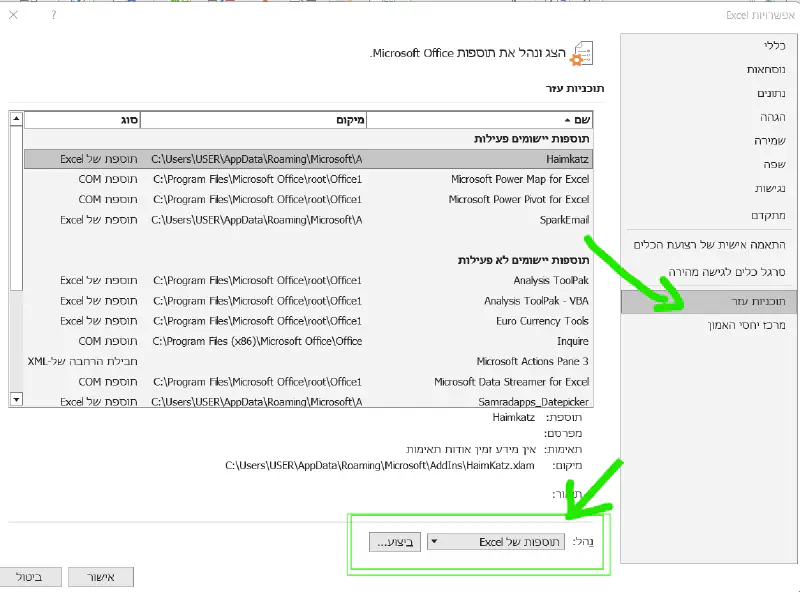
• בתחתית מסך האפשרויות ישנו מקום בו כתוב בו נהל: תוספות של Excel (באנגלית: Manage (adds ins**,** ולצידו יש כפתור ביצוע… Go.
  נלחץ על כפתור ביצוע… Go.
• במסך הקטן שיפתח, נסמן את Analysis Toolpack ונלחץ על אישור.

מרגע זה, בתפריט נתונים Data מופיע לנו גם חלק חדש שנקרא Analysis ובתוכו כפתור Analysis Toolpack .

איך לחשב רגרסיה ליניארית באקסל עם Analysis Toolpack ? 🏁

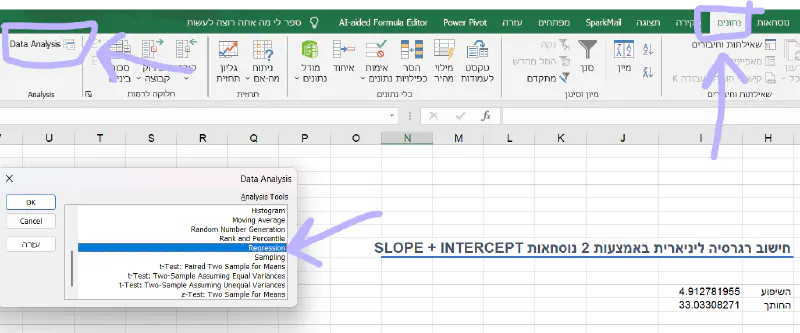
• נלחץ על לשונית נתונים Data
• ואז על כפתור Analysis Toolpack 🧰,
• ובחלון שיפתח נוכל לבחור את הניתוח הרצוי.
• כיוןן שאנחנו עוסקים ברגרסיה, נבחר ב Regression 📉

ואז יפתח מסך שבו נוכל להגדיר את הנתונים שצריך לצורך חישוב הרגרסיה (=קלט).

• בשדה Input Y Range נשים את טווח התאים שמכילים את המשתנה המוסבר, מה שרוצים לחזות.
• בשדה Input X Range נשים את טווח התאים שמכילים את המשתנה המסביר , זה שלדעתנו גורם לשינוי.
• ואז נבחר באפשרות Output Range - כלומר, ניתוח הרגרסיה יתחיל בתא שנבחר.
  נבחר תא שבו התוסף יתחיל לכתוב את כל המדדים ופרטי ניתוח רגרסיה.
• אחרי שנלחץ אישור נקבל מספר טבלאות.

איך מרכיבים את נוסחת הרגרסיה הליניארית מתוך הטבלאות של Analysis Toolpack? 🧑‍🔬

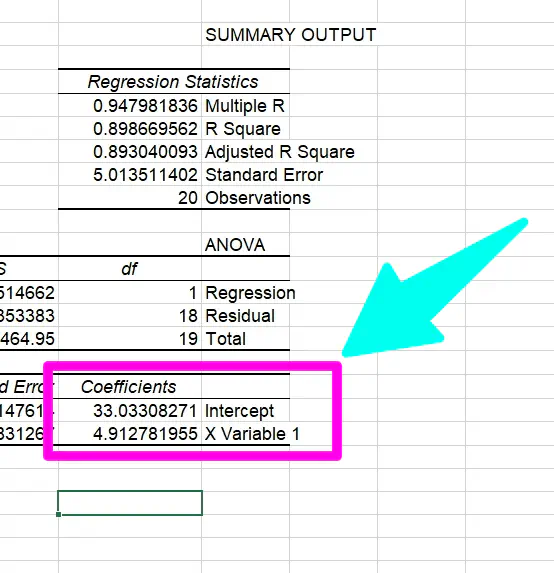
כדי לקבל את הערכים של הנוסחה, פשוט מסתכלים על הטבלה השלישית, בעמודה Coefficients.
החותך זה הערך הראשון, לצד המילה Intercept
והשיפוע זה הערך השני.

הסבר המדדים הסטטיסטיים של ניתוח רגרסיה ליניארית 📏

היתרון הגדול שנותן לנו התוסף Analysis Toolpack ביצירת רגרסיה ליניארית, הוא – שהוא נותן גם את כל המדדים הסטטיסטים הנחוצים לנו כדי שנוכל להעריך עד כמה הרגרסיה הליניארית הזאת טובה, והאם היא מסוגלת אכן לחזות בסיכוי סביר את המשתנה המוסבר.
בשתי השיטות הקודמות שהראתי לעשות רגרסיה ליניארית באקסל, לא מקבלים את המדדים האלו. זהו חיסרון גדול, מכיוון שכאשר אנחנו עושים ניתוח רגרסיה ליניארית, נרצה תמיד לדעת האם אפשר לסמוך על הרגרסיה הליניארית הזאת, כלומר במילים אחרות, האם הקשר שאנחנו משערים שיש בין המשתנה מסביר למשתנה המוסבר באמת קיים.
הרי ברור לחלוטין שיכולים להיות מקרים שבהם אנחנו משערים שמשתנה מסוים מסביר משתנה אחר, אבל כשבודקים את זה, מוצאים שבכלל אין קשר ביניהם צריך סוגריים כלומר אולי קיים קשר אבל הוא חלש מאוד ולכן לא ניתן להתייחס לקשר הזה בתור משהו סביר לצורך תחזית).

לצורך כך, התוסף מייצר עבורנו את טבלת Regression Statistics שמכילה מספר מדדים סטטיסטיים על הרגרסיה.
לכן כעת, נעבור ביחד על המדדים הסטטיסטים השונים של רגרסיה ליניארית, נתמקד במדדים העיקריים, שיאפשרו לנו לענות על השאלה: האם המודל רגרסיה ליניארית במקרה שלנו מנבא היטב?

לפני שנתחיל, אני רוצה לסכם רשימה של כללים (כללי אצבע) שמאפשרים להחליט במהירות, האם הרגרסיה טובה או לא, גם למי שלא מבין. לאחר פירוט הכללים, נדבר על כל מדד בנפרד.

האם המודל רגרסיה ליניארית מנבא היטב? ✅

כדי להיות בטוח שהרגרסיה ליניארית שאקסל נתן לך היא טובה מספיק, ואתה יכול לעשות החלטה הגיונית מבחינת סטטיטיסית ולהשתמש בה, אז המצב צריך להיות כזה:

• Multiple R גדול מ מ 0.7
• R Square גדול מ 0.7
• Standard Error קטן במונחים של מה שאתה מודד
• Significance F הכי טוב אם הוא קטן מ 0.01 (כלומר 1%), אך גם אם עוברים אותו, לא יותר מ- 0.05 (כלומר 5%).

כלומר, אם היה לך רעיון שמשתנה מסויים משפיע מאוד על רווחי העסק שלך (או כל קשר אחר בין משתנים בעבודה שלך), ועשית לו ניתוח רגרסיה ליניארית, וכל המדדים שציינתי עומדים בכללי האצבע שפירטתי,

אם כן - אתה יכול בביטחון להתקדם עם המודל הזה, ולחזות איתו. 🚦

אם לא - ההשערה על הקשר בין הדברים אינה נכונה, ועליך לוותר על המודל. ❌

וכעת נעבור להסביר את המדדים עצמם.

מדד Multiple R עבור רגרסיה ליניארית

• מדד Multiple R הוא מדד לעוצמת הקשר בין המשתנים.
  • מספר קרוב ל-1 - יש קשר חזק בין המשתנים. ובאמת המשתנה המסביר - משפיע על המשתנה המוסבר, בדוגמה שלנו, הטמפרטורה אכן משפיעה על כמות הגלידות הנמכרות.
  • מספר קרוב ל-0 - הקשר בין המשתנים חלש או גרוע ביותר.
  • אנחנו רוצים קשר חזק. רוצים מספר קרוב ל-1.
  • אם למשל המספר הוא 0.2 - הרגרסיה לא נכונה, ופשוט נבין שאין קשר בין המשתנים.
  • אם למשל המספר הוא 0.7 - הרגרסיה הליניארית טובה, יש קשר ליניארי חזק בין המשתנים, ומבחינתנו זה יהיה מספיק הגיוני להשתמש בנוסחת רגרסיה כדי לנסות לחזות דברים.

הרחבה למעוניינים: מדד Multiple R מייצג את הקשר בין המשתנים הבלתי תלויים (המסבירים) למשתנה התלוי. מדד Multiple R הוא ערך מוחלט של הקורלציה (מקדם המתאם של פירסון) בין המשתנה המוסבר למשתנה המסביר. כידוע, קורלציה נעה בין -1 ל- +1, אבל כיוון ש Multiple R הוא ערך מוחלט של הקורלציה, לכן, ערכו נע בין 0 ל-1. כאשר 1 מציין קשר מושלם ואילו כאשר הוא 0 זאת אומרת שאין קשר בכלל בין המשתנים. כיוון שזה ערך מוחלט של מקדם המתאם, אז אנחנו לא יכולים לדעת אם הקשר בין המשתנים הוא חיובי (ככל שאחד עולה, גם השני עולה) או שלילי (ככל שאחד עולה, השני יורד), אבל אנחנו כן יכולים לדעת את עוצמת הקשר, כפי שציינתי, לפני כן, אם הוא קרוב ל-1 זה קשר טוב, ולהיפך, אם הוא קרוב לאפס - הקשר חלש עד בלתי קיים. כלומר, מדד Multiple R מציין עד כמה הקשר בין המשתנים חזק, הוא נותן מספר שמאפשר לנו להעריך עד כמה המשתנים זזים במשותף. עד כמה הם “רוקדים” יחד.

מדד R-Square - מדד R בריבוע עבור רגרסיה ליניארית

• מדד R-Squared מודד עד כמה קו הרגרסיה קרוב לנתוני האמת.
• גם R-Square יכול לנוע בין 0 ל-1.
• גם R-Square בציון קרוב ל-1 זה טוב, ובציון קרוב ל-0 זה גרוע. בניסוח חופשי, אפשר לומר שהוא נותן ציון לקו רגרסיה שלנו.
• נניח, יצא 0.6 (כלומר ציון של 60%), זה אומר ש-60% מהשינוי במשתנה המוסבר (התחזית) - מקורו במשתנה המסביר שלנו.
• R Square אומר לנו כמה טוב המודל מסביר את הנתונים. כמה טובה נוסחת הרגרסיה שלנו.

דוגמה להמחשת המשמעות של R Squared, מדד R בריבוע על רגרסיה ליניארית

לדוגמא, כשאנחנו בוחנים כמות מכירות של מוצר. ידוע לנו שישנם מרכיבים רבים שמשפיעים על כמות היחידות שנמכרות מאותו מוצר:

• איכות המוצר
• מה עושים המתחרים (אם מתחרה מסויים התחיל בדיוק מבצע, זה עשוי להשפיע גם על המכירות של המוצר שלנו)
• מצב הכלכלה (אם כרגע יש מיתון, זה משפיע על מכירות
• וכמובן - פרסום.

אז כאשר ניצור מודל רגרסיה שמנסה לחזות את השפעת הפרסום על כמות המכירות של המוצר, מדד R-Squared אומר לנו איזה חלק מהשינוי במכירות נובע ישירות מהפרסום (ולא משאר הגורמים האפשריים).

אם למשל עשינו ניתוח רגרסיה לינארית באקסל, וקיבלנו ערך R-Squared של 0.85.
אז פירוש הדבר ש-85% מהשונות במכירות מוסברת על ידי תקציב הפרסום. כלומר, רוב ההשפעה על השינוי במכירות נובעת מהפרסום, בעוד ש-15% הנותרים מושפעים מגורמים אחרים כמו איכות המוצר, פעילות המתחרים או מצב הכלכלה.

עם זאת, חשוב לציין כי R Square פועל כמתוכנן רק במודל רגרסיה ליניארי פשוט עם משתנה מסביר אחד. אם יש לנו מקרה של רגרסיה מרובה עם מספר משתנים בלתי תלויים, יש להתאים את ה-R Square, וזה בדיוק מה שעושה המדד הבא : Adjusted R Squared, ולא ארחיב עליו, כיוון שאני רוצה להתמקד במקרה הפשוט .

מדד Stardard Error של רגרסיה ליניארית

זה מדד ממש פשוט, שהמשמעות שלו היא כמה המודל טועה בממוצע ביחס למציאות.
למשל, בדוגמה עם הטמפרטורה והגלידות, יצא Standard Error של 5.01, זאת אומרת, שבממוצע נוסחת הרגרסיה טועה ב-5 גלידות ביחס למציאות (ב-95% מהפעמים).
במילים אחרות, ההבדל בין המספר שנקבל מהרגרסיה הליניארית למספר האמיתי במציאות, כלומר התחזית תסטה מהערך האמיתי, ברוב הפעמים, ב 5 גלידות לכאן או לכאן.

מדד Significance F של רגרסיה ליניארית

גם המדד הזה ממש פשוט, והמשמעות שלו היא מה הסיכוי (באחוזים) שמודל הרגרסיה שלנו הוא שגיאה לחלוטין. ברור שאנחנו מחפשים מספר נמוך ככל האפשר. מקובל לדבר במושגים של 1% או פחות - זה מעולה, 5% בגדר הסביר, ו-10% זה לא טוב.

סיכום - רגרסיה ליניארית ב-Excel 🏆

למדנו מהי הרגרסיה הליניארית, בתור כלי סטטיסטי שימושי ונגיש. ראינו איך כל מי שמעוניין לקבל החלטות מבוססות נתונים במקום להסתמך על ניחושים. ראינו דוגמאות מעשיות, כמו ניתוח מכירות גלידה לפי טמפרטורה ומיקוד קמפיינים שיווקיים בחנות אונליין. המחשנו כיצד רגרסיה חושפת קשרים בין משתנים ומאפשרת לחזות תוצאות. התמקדתי ביישום הכי פשוט של רגרסיה באמצעות תוכנת אקסל, וסקרנו יחד שלוש שיטות לביצוע רגרסיה ליניארית עם Excel, כאשר אני ממליץ חד משמעית על השימוש בתוסף Analysis Toolpack. הסיבה לכך היא שהתוסף מספק מדדי אמינות חיוניים (כמו Multiple R, R Square ו-Significance F).
בנוסף, ואולי הכי חשוב, נתתי מספר “כללי אצבע” ברורים ופשוטים שכל מי שמיישם אותם יכול לסמוך על ניתוח רגרסיה ליניארית שיצא לו.
אני מקווה שהסרתי עבורכם את המסתורין מהמונח רגרסיה ליניארית והפכתי אותה לכלי מעשי שכל אחד יכול להשתמש בו כדי להבין טוב יותר את הגורמים המניעים את העסק שלו ולחסוך כסף.

📝 הבהרה לחובבי הסטטיסטיקה שבקהל:
אם הרמתם גבה על כך שלא דיברתי על P-value של כל משתנה – תנשמו עמוק, זה לא בגלל ששכחתי את זה.
פשוט בחרתי להישאר בגזרה הפשוטה של רגרסיה ליניארית עם משתנה מסביר אחד. שהיא גם המקרה הנפוץ במציאות של עסקים. במילים אחרות: כשיש רק X אחד במשוואה – אין צורך להפוך כל מקדם לדרמה סטטיסטית שלמה. (כמובן, שאם אתם בניתוח רגרסיה עם משתנים רבים – אל תוותרו על בדיקת P-values בנפרד. לא כל משתנה הוא תורם פעיל, גם אם נראה עסוק 🙂)